Backpropagation

Use partial derivative chain rule to link the loss to the target parameter.

Essence

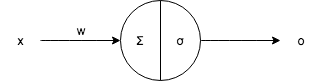
For any hidden layer neuron:

$$ \begin{aligned} \frac{\partial \mathcal{L}}{\partial W'} &= \left( \frac{\partial \mathcal{L}}{\partial o'} \cdot \frac{\partial o'}{\partial \sigma} \cdot \frac{\partial \sigma}{\partial \Sigma'} \right) \cdot \frac{\partial \Sigma'}{\partial W'} \\ &= \left( \delta' \right) \cdot o \end{aligned} $$

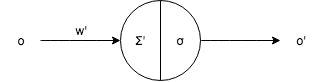
For its previous neuron:

$$ \begin{aligned} \frac{\partial \mathcal{L}}{\partial W} &= \left( \frac{\partial \mathcal{L}}{\partial o} \cdot \frac{\partial o}{\partial \sigma} \cdot \frac{\partial \sigma}{\partial \Sigma} \right) \cdot \frac{\partial \Sigma}{\partial W} \\ &= \left( \delta \right) \cdot x \end{aligned} $$

where $$ \begin{aligned} \frac{\partial \mathcal{L}}{\partial o} &= \sum \left( \frac{\partial \mathcal{L}}{\partial \Sigma'} \right) \cdot \frac{\partial \Sigma'}{\partial o} \\ &= \sum (\delta') \cdot W' \end{aligned} $$

Note:

• We only need to store $\sigma, \frac{\partial \sigma}{\partial \Sigma}$ during forward phase.
• $\delta = \frac{\partial \mathcal{L}}{\partial \Sigma}$ is a temporary variable for computational convenience during backward phase.
• $\Sigma​$ all errors of the forward layer's neurons during backward phase.

From Scratch

class NeuralNetwork(object):
    """Properties:
        layers::int
        W::[numpy.matrix], b::[numpy.vector]
        Σ::[numpy.vector] -> dfdΣ::[numpy.vector]
        o::[numpy.vector]
        δ::numpy.vector
    """
    def __init__(self, sizes):
        """[numpy.matrix] -> NerualNetwork"""
        self.W = [
            numpy.matrix(numpy.random.randn(k_out, k_in)) 
            for k_in, k_out in zip(sizes[:-1], sizes[1:])
        ]
        self.b = [
            numpy.random.randn(k) 
            for k in sizes[1:]
        ]
        self.layers = len(sizes)
        self.dfdΣ = deque(maxlen=self.layers-1)  # self.Σ
        self.o = deque(maxlen=self.layers)

    def forward(self, x, f, df):
        """numpy.vector, f, f -> numpy.vector"""
        self.o.append(x)
        for W, b in zip(self.W, self.b):
            Σ = W * self.o[-1] + b
            self.o.append(f(Σ))
            self.dfdΣ.append(df(Σ))  # self.Σ.append(Σ)
        return self.o[-1]

    def backward(self, y, dE):
        """numpy.vector, f, f -> [numpy.matrix], [numpy.vector]"""
        dEdW, dEdb = [], []
        for i in -numpy.arange(1, self.layers):
            if i == -1:
                δ = dE(y, self.o[i]) * self.dfdΣ[i]
            else:
                δ = (δ * self.W[i]) * self.dfdΣ[i]
            dEdW.append(numpy.matrix(δ).T * self.o[i - 1])
            dEdb.append(δ)
        return reversed(dEdW), reversed(dEdb)

    def update(self, ɑ, dEdW, dEdb):
        """float, [numpy.matrix], [numpy.vector] -> Side-Effect"""
        for i in range(self.layers):
            self.W[i] -= ɑ * dEdW[i]
            self.b[i] -= ɑ * dEdb[i]

by Jon